| 5.9: Exercises | 您所在的位置:网站首页 › kelly graph › 5.9: Exercises |
5.9: Exercises
|
13. Find the chromatic number of the graph \(G\) in Figure 5.52 and a coloring using \(\chi(G)\) colors. 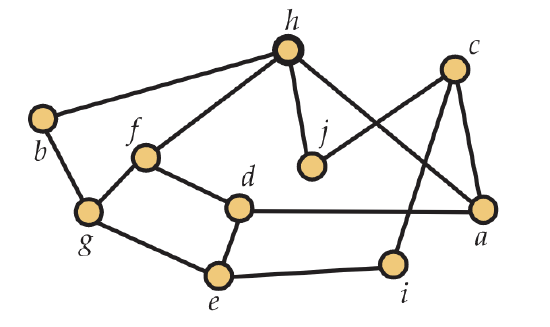 Figure 5.52. A graph \(G\) to color Figure 5.52. A graph \(G\) to color
14. Find the chromatic number of the graph \(G\) in Figure 5.53 and a coloring using \(\chi(G)\) colors. 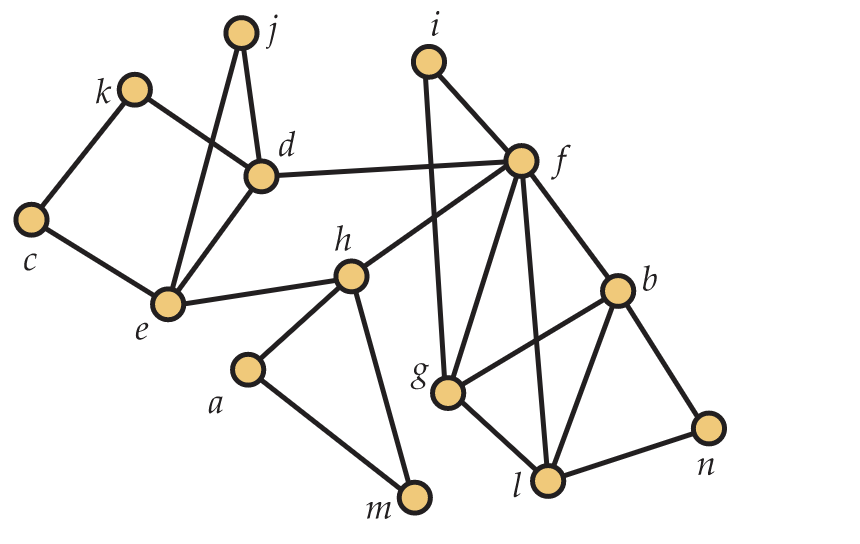 Figure 5.53. A graph \(G\) to color Figure 5.53. A graph \(G\) to color
15. A pharmaceutical manufacturer is building a new warehouse to store its supply of 10 chemicals it uses in production. However, some of the chemicals cannot be stored in the same room due to undesirable reactions that will occur. The matrix below has a 1 in position \((i,j)\) if and only if chemical \(i\) and chemical \(j\) cannot be stored in the same room. Develop an appropriate graph theoretic model and determine the smallest number of rooms into which they can divide their warehouse so that they can safely store all 10 chemicals in the warehouse.
16. A school is preparing the schedule of classes for the next academic year. They are concerned about scheduling calculus, physics, English, statistics, economics, chemistry, and German classes, planning to offer a single section of each one. Below are the lists of courses that each of six students must take in order to successfully graduate. Determine the smallest number of class periods that can be used to schedule these courses if each student can take at most one course per class period. Explain why fewer class periods cannot be used. Student Courses 1 Chemistry, Physics, Economics 2 English, German, Statistics 3 Statistics, Calculus, German 4 Chemistry, Physics 5 English, Chemistry 6 Chemistry, Economics17. All trees with more than one vertex have the same chromatic number. What is it, and why? 18. Find a proper \((t+1)\)-coloring of the graph \(G_{t+1}\) in Mycielski's proof of Proposition 5.25. This establishes that \(\chi(G_{t+1}) < t+1\). 19. How many vertices does the graph \(G_4\) from the Kelly and Kelly proof of Proposition 5.25 have? 20. Construct and draw the graph \(G_5\) from Mycielski's proof of Proposition 5.25. 21. Find a recursive formula for the number of vertices nt in the graph \(G_t\) from the Kelly and Kelly proof of Proposition 5.25. 22. Let \(b_t\) be the number of vertices in the graph \(G_t\) from the Mycielski's proof of Proposition 5.25. Find a recursive formula for \(b_t\). 23. The girth of a graph \(G\) is the number of vertices in a shortest cycle of \(G\). Find the girth of the graph \(G_t\) in the Kelly and Kelly proof of Proposition 5.25 and prove that your answer is correct. As a challenge, see if you can modify the construction of \(G_t\) to increase the girth. If so, how far are you able to increase it? 24. Use the First Fit algorithm to color the graph in Figure 5.26 using the two different orderings of the vertex set shown there. 25. Draw the interval graph corresponding to the intervals in Figure 5.54. 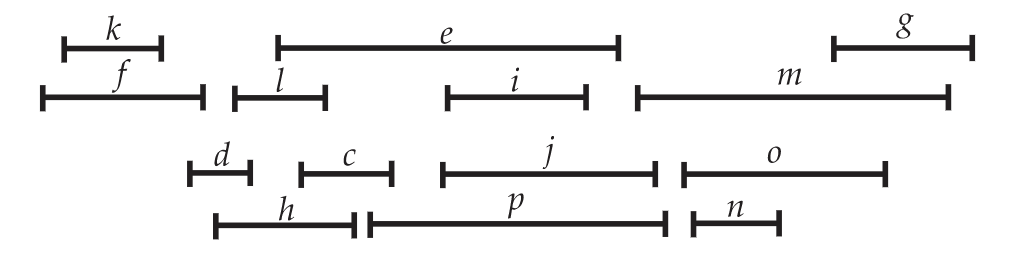 Figure 5.54. A collection of intervals Figure 5.54. A collection of intervals
26. Use the First Fit coloring algorithm to find the chromatic number of the interval graph whose interval representation is shown in Figure 5.54 as well as a proper coloring using as few colors as possible. 27. a. From Exercise 5.9.24 you know that choosing a bad ordering of the vertices of a graph can lead to the First Fit coloring algorithm producing a coloring that is far from optimal. However, you can use this algorithm to prove a bound on the chromatic number. Show that if every vertex of \(G\) has degree at most \(D\), then \(\chi(G) \leq D + 1\). b. Give an example of a bipartite graph with \(D=1000\) to show that this bound need not be tight. 28. Is the graph in Figure 5.53 planar? If it is, find a drawing without edges crossings. If it is not give a reason why it is not. 29. Is the graph in Figure 5.55 planar? If it is, find a drawing without edge crossings. If it is not give a reason why it is not. 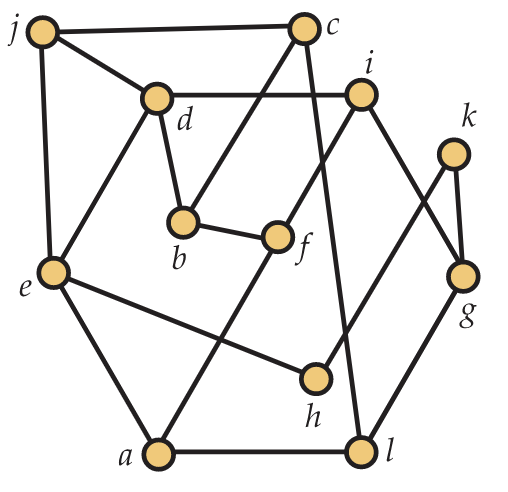 Figure 5.55. Is this graph planar? Figure 5.55. Is this graph planar?
30. Find a planar drawing of the graph \(K_{5−e}\), by which we mean the graph formed from the complete graph on 5 vertices by deleting any edge. 31. Exhibit a planar drawing of an eulerian planar graph with 10 vertices and 21 edges. 32. Show that every planar graph has a vertex that is incident to at most five edges. 33. Let \(G=(V,E)\) be a graph with \(V=\{v_1,v_2,…,v_n\}\). Its degree sequence is the list of the degrees of its vertices, arranged in nonincreasing order. That is, the degree sequence of \(G\) is \((deg_G(v_1),deg_G(v_2),…,deg_G(v_n))\) with the vertices arranged such that \(deg_G(v_1) \geq deg_G(v_2) \geq \cdot \cdot \cdot \geq deg_G(v_n). Below are five sequences of integers (along with \(n\), the number of integers in the sequence). Identify the one sequence that cannot be the degree sequence of any graph the two sequences that could be the degree sequence of a planar graph the one sequence that could be the degree sequence of a tree the one sequence that is the degree sequence of an eulerian graph the one sequence that is the degree sequence of a graph that must be hamiltonianExplain your answers. (Note that one sequence will get two labels from above.) a. \(n=10: (4,4,2,2,1,1,1,1,1,1)\) b. \(n=9: (8,8,8,6,4,4,4,4,4)\) c. \(n=7: (5,4,4,3,2,1,0)\) d. \(n=10: (7,7,6,6,6,6,5,5,5,5)\) e. \(n=6: (5,4,3,2,2,2)\) 34. Below are three sequences of length .10. One of the sequences cannot be the degree sequence (see Exercise 5.9.33) of any graph. Identify it and say why. For each of the other two, say why (if you have enough information) a connected graph with that degree sequence is definitely hamiltonian/cannot be hamiltonian is definitely eulerian/cannot be eulerian is definitely a tree/cannot be a tree is definitely planar/cannot be planar(If you do not have enough information to make a determination for a sequence without having specific graph(s) with that degree sequence, write “not enough information” for that property.) a. \((6,6,4,4,4,4,2,2,2,2)\) b. \((7,7,7,7,6,6,6,2,1,1)\) c. \((8,6,4,4,4,3,2,2,1,1)\) 35. For the two degree sequences in Exercise 5.9.34 that correspond to graphs, there were some properties for which the degree sequence was not sufficient information to determine if the graph had that property. For each of those situations, see if you can draw both a graph that has the property and a graph that does not have the property. 36. Draw the 16 labeled trees on 4 vertices. 37. Determine prüfer(T) for the tree \(T\) in Figure 5.56. 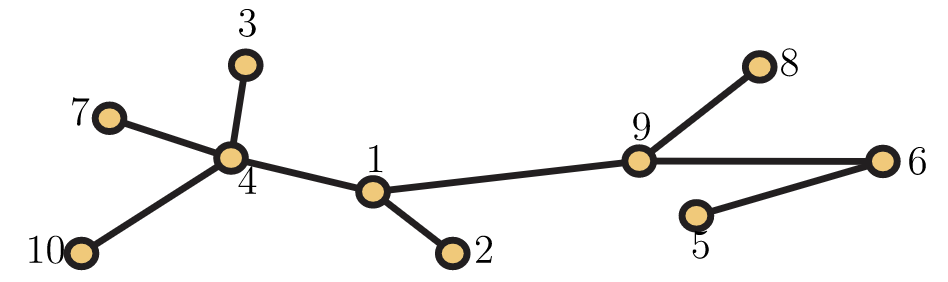 Figure 5.56. A 10-vertex tree Figure 5.56. A 10-vertex tree
38. Determine prüfer(T) for the tree \(T\) in Figure 5.57. 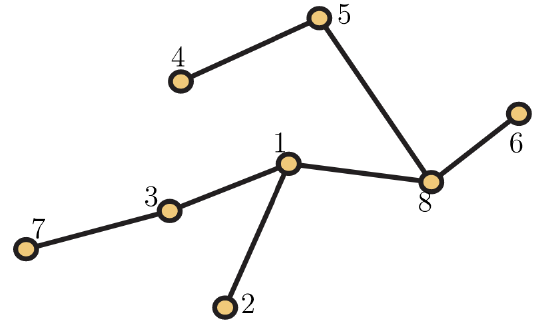 Figure 5.57. A 10-vertex tree Figure 5.57. A 10-vertex tree
39. Determine prüfer(T) for the tree \(T\) Figure 5.58. 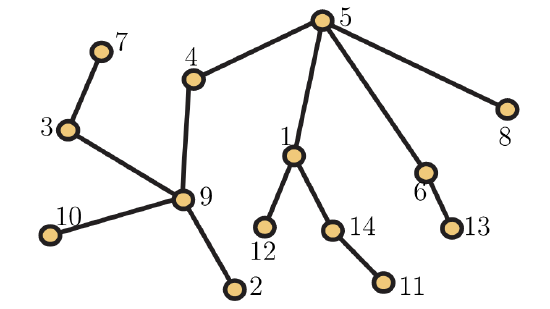 Figure 5.58. A 14-vertex tree Figure 5.58. A 14-vertex tree
40. Construct the labeled tree \(T\) with Prüfer code 96113473. 41. Construct the labeled tree \(T\) with Prüfer code 23134. 42. Construct the labeled tree \(T\) with Prüfer code (using commas to separate symbols in the string, since we have labels greater than 9) \(10,1,7,4,3,4,10,2,2,8\) 43. (Challenge Problem) When \(G=(V,E)\) is a graph, let \(Δ(G)\) denote the maximum degree in \(G\). Prove Brooks' Theorem: If \(G\) is connected and \(Δ(G)=k\), then \(\chi(G) \leq k+1\). Furthermore, equality holds if and only if (a) \(k=2\) and \(G\) is an odd cycle, or (b) \(k \neq 2\) and \(G = K_{k+1}\). HintIt's clear that \(\chi(G) \leq k+1\) (in fact, this was already assigned as an exercise). Assume that \(\chi(G)=k+1\) but that neither conclusion (a) or (b) holds. Take a spanning tree of \(G\) and an appropriate ordering of the vertices, with two leaves of the tree coming first. Then show that a First Fit coloring of the graph will only use \(k\) colors. |
【本文地址】
